-




-
Probability
It’s time to introduce some concepts from statistical theory. The collection of all possible elementary outcomes of an experiment is called the sample space, Ω. The sample space of our experiment is the natural numbers Ω={1,2, 3 …}, a countably infinite set. An event, E is a subset of the sample space. The probability of getting Yahtzee in three or fewer tosses represents the event E = {1,2,3}. The sample space can be a discrete set, finite or countably infinite but it can also be continuous and uncountable such as the real numbers,
 .
.In a sequence of trials in an experiment such as ours the number of times a particular event E occurs is called its frequency. The ratio of that frequency to the number of trials is the relative frequency. The relative frequency of E tends to stabilize as the number of trials increase. This is illustrated in the applet. The limit is called the probability P of E. P is assumed to be the likelihood of a certain outcome in a single trial.
A Probability space (Ω,
 , P)
is a sample space Ω, a collection of subsets i.e. events
, P)
is a sample space Ω, a collection of subsets i.e. events
 and a
probability assignment P to each event. The collection
and a
probability assignment P to each event. The collection  must technically be a Borel field of subsets. Normally it’s just the collection of all subsets of Ω.
The probability assignment to events must satisfy three axioms.
must technically be a Borel field of subsets. Normally it’s just the collection of all subsets of Ω.
The probability assignment to events must satisfy three axioms.1. P(Ω)=1
2. 0≤P(E)≤1
3. P(∪iEi) = ∪i P(Ei) for every sequence of disjoint events Ei
For a discrete sample space such as N={1,2,3…} each point can be assigned a probability. The probability of an event will be the sum of the parts P(E)=ΣωP(ω) summing over all ω
 E. This obviously doesn’t work for
continuous spaces such as
E. This obviously doesn’t work for
continuous spaces such as  , where probabilities must
be assigned to events like intervals instead of individual points. Assignment of probabilities
to events can be thought of as a distribution of the total probability that equals one, among points and regions
of the sample space.
, where probabilities must
be assigned to events like intervals instead of individual points. Assignment of probabilities
to events can be thought of as a distribution of the total probability that equals one, among points and regions
of the sample space.A random variable is a function X(ω) defined on a probability space with values in a value space X⊆
 . If the sample space is
the points in the unit disc Ω= { (x,y)
. If the sample space is
the points in the unit disc Ω= { (x,y)
 2
| (x2+y2) ≤1 } then distance from the origin would be a random variable X(ω)=
2
| (x2+y2) ≤1 } then distance from the origin would be a random variable X(ω)=
 .
When the sample space is part of
.
When the sample space is part of  it is natural to use the
random variable X(ω)=ω.
it is natural to use the
random variable X(ω)=ω.The random variable X(ω) provides a natural transfer of probabilities from sample space to a value space of real numbers. P(A)=P( { ω | X(ω)
 A} ). For a discrete random variable
with values xi the probabilities are described by the probability
function p(xi).
A} ). For a discrete random variable
with values xi the probabilities are described by the probability
function p(xi).The distribution function is used to characterize the distribution of probabilities for a random variable. It is defined as F(λ)=P( { ω | X(ω )≤λ} ). The distribution function F(λ) of a random variable sweeps up probability from −∞ to +∞. It is also called the cumulative distribution function c.d.f. F(λ) is a non-decreasing function with F(−∞)=0 and F(+∞)=1.
The distribution F(λ) of the random variable describing distance from the origin gives the probability for a point to be at a distance less than λ based on a uniform probability distribution over the unit disc, i.e. equal areas have the same probability.
 Check this!
Check this!The probability of a random variable being in a certain interval is given by:
P( a<x≤b ) = F(b) – F(a).
A possible déjà vu could be caused by :
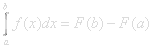
The derivative function f(λ)=F’(λ) of the c.d.f of a continuous variable is called the density function. If probability is like a unit mass distributed over a certain space then the density function would represent density of mass. It’s the continuous version of the probability function.
If you conduct a large number of trials in a chance experiment with k possible outcomes x1,x2,... xk and probabilities p1,p2,...pk then you would expect the average value of all outcomes to be Σxipi.
The expected value of a random variable X is:
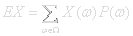
Expected value can be a misleading term. The value might not even exist in the value space of X. A electron spin direction experiment with X=1 for up and X=0 for down could have an expected value of ½ even though every electron is detected as either up or down. Expected value is analogous to center of gravity for a mass distribution.
The operation of calculating expectation values for a random variable is linear. Given two random variables X(ω),Y(ω) and forming a new one Z(ω)=aX(ω)+bY(ω) gives:
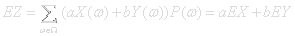
The expectation value of a random variable X(x)=x on a sample space in
 is:
is: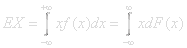
f(x)is the density function and F(x) is the distribution function.
The information in the density function for a random variable is often summarized with a few numbers. The most important are the expectation value, μ=EX and μ2=E( (X-μ)2 ) also called the central moment of order 2. μ2 is related to the amount of spread in a distribution. μ3= E( (X-μ)3 ) has to do with skewness, asymmetry in the distribution. Under normal conditions the distribution will be uniquely defined by its moments μ, μ2, μ3, . . . .
The spread in a distribution of a random variable is called variance.
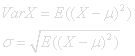
σ is called the standard deviation of X.
Another measure of spread would be the mean deviation E( |X-μ| ). The downside of this is that taking the absolute value is not a continuous operation which complicates analysis.
Note that the expectation value of X2 doesn’t equal μ2. EX2 - μ2 = Var X2 (Show this!). Here’s another exercise, calculate the density function, expectation value and standard deviation of the random variable X(ω)=
 .
in the unit disc example.
.
in the unit disc example.